Now Inhale

This is the second story Eric Frank Russell has written about an earthman using mathematics cleverly to escape alien imprisonment (the first was “Diabologic”)

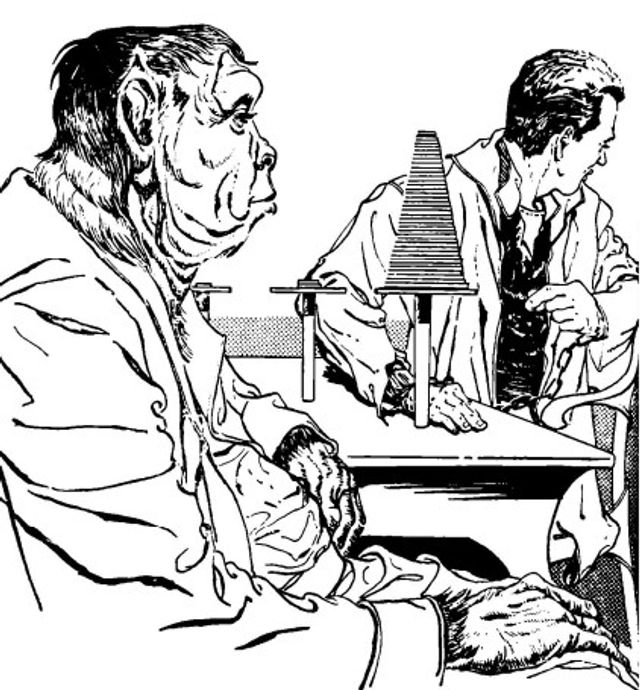
The Gamborians have captured the space-faring Wayne Taylor, and as is their custom, he is set to die - no appeals. But before dying, the prisoner gets to play 1 game with a Gamborian, sort of a “last meal” ritual . It does not matter who wins or loses, for the prisoner is destined to be executed, but as long as the game goes on, the prisoner lives. The Gamborians honor this tradition and do not cheat or try to use force to subjugate the opponent in this Final Game.

So then, our friend Wayne tells them about a game called “Arky Malarkey” played by priests on earth, involving 3 pegs, 64 disks, some rules governing the movement of the disks (you can move only one plate at a time and at no time can a larger plate be on top of a smaller plate) … and a very humorous story unfolds. It is a really enjoyable read.

The game, of course, is the well-known “Tower of Hanoi”, the classic math puzzle invented in 1883 by the puzzle-master, Edouard Lucas. The story takes off from a brief comment by the French writer, Henri de Parville, in 1884, when he spiced up the puzzle with an intriguing, mystical thought as follows (which was later repeated in Rouse Ball’s book and then most famously in Kasner’s “Mathematics & Imagination”)”

“In the great temple of Benares, under the vault marking the center of the world, rests a bronze plate in which three diamond needles are placed, each one of one cubit high, and as wide as the body of a bee. On one of these needles, God, in Creation, placed 64 pure gold discs; the largest disc rested on the bronze plate, and the others, in decreasing order of diameter were placed successively until the top one was reached. This is the tower of Brahma. Day and night priests transfer the disks from one : diamond needle to another, constantly, according to the fixed laws and immutable Brahma, demanding that the priest in charge should not move more than one plate at a time, and should place this plate on a needle so that there is no smaller plate below it. When the 64 discs have thus been transferred to one of the other needles from the needle on which God, in Creation, placed them, then the tower, the temple, and the Brahmans, alike, will disintegrate into dust, and in a thunder the world disappear”.

With 3 spindles and n disks, the minimum number of moves to accomplish the task is 2^n-1, a result easily proved using mathematical induction (though the problem using more than 3 spindles remains open as far as I know (Thierry Bousch had apparently verified an optimal algorithm in 2014, though Wolfram mathworld site continues to list it as an open issue)

Further Commentary: Alex Kasman had raised an objection to having this story categorized as mathfiction, since the presence of a game or its analysis does not automatically constitute “mathfiction”. I don’t disagree with him that ‘the game does not mathfiction make’, otherwise every story involving poker or chess would have to be included, for example. However, a very specific problem like “Tower of Hanoi” has a special place, in my opinion, because it is very niche, is commonly used in teaching a very specific mathematical technique like induction and recursion, and such stories are not very common. So when I first read this story, there was an automatic bulb of “mathfiction” which went off in my mind and I did not even hazard a second guess till Alex raised his (valid) objection.

So I suppose there is some amount of artistic license of judgment involved in categorizing this as mathfiction, and I do believe that inclusion helps a mathematical discussion for those who come across it.